Tiempo de lectura estimado: 5 minutos
Tabla de contenidos
Los números son una parte esencial de nuestra vida cotidiana, y dentro de ese vasto mundo numérico, existen los números racionales. ¿Alguna vez te has preguntado qué son exactamente los números racionales y cómo se diferencian de otros tipos de números? En este artículo, te llevaré en un emocionante viaje al mundo de los números racionales, desde su definición hasta su origen histórico y ejemplos prácticos. Prepárate para desentrañar el misterio de los números racionales y descubrir cómo se aplican en situaciones de la vida real.
El Concepto de Número Racional
Comencemos por definir qué son los números racionales. En términos simples, un número racional es cualquier número que se puede expresar como el cociente (división) de dos números enteros, donde el denominador (el número de abajo) no es igual a cero. Los números racionales pueden ser positivos o negativos, enteros o fracciones.
La forma general de un número racional es:
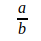
Donde "a" es el numerador (el número de arriba) y "b" es el denominador (el número de abajo). Aquí, "a" y "b" son enteros, y "b" no puede ser igual a cero.
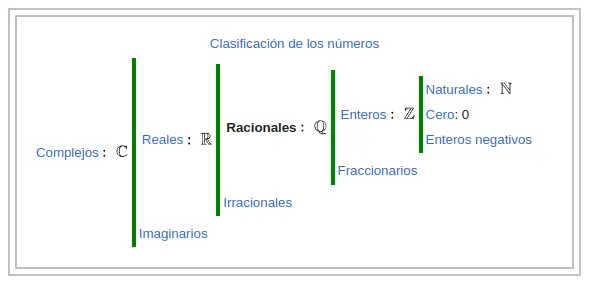
Origen de los Números Racionales
Los números racionales tienen una larga historia que se remonta a la antigua Grecia. Los matemáticos griegos como Pitágoras y Euclides ya estudiaban números_racionales hace más de 2,000 años. Sin embargo, fue el matemático griego más famoso, Euclides, quien proporcionó una definición rigurosa de números_racionales en sus «Elementos». Euclides demostró que, dados dos números primos, uno de ellos debe ser divisor del otro, lo que establece la base para la representación de números racionales como fracciones.
Los egipcios, en su búsqueda por resolver problemas prácticos, empleaban fracciones con denominadores enteros positivos. Estas fracciones representaban las ‘partes de un entero’ y se basaban en el concepto de números_racionales. Por otro lado, los matemáticos de la antigua Grecia desarrollaron la idea de conmensurabilidad, que establecía que dos magnitudes eran conmensurables si se podía encontrar una tercera magnitud que fuera múltiplo de ambas. Esto implicaba que existía una unidad común que permitía medir ambas magnitudes de manera entera. Este principio pitagórico, que afirmaba que cualquier número podía expresarse como un cociente de enteros, resaltaba la noción de números_racionales.
El término ‘racionales’ se deriva etimológicamente del latín ‘ratio’, que significa ‘razón‘, y del griego ‘λόγος’ (razón), utilizado por los matemáticos griegos antiguos para referirse a estos números. Así, ‘números_racionales’ se traduce literalmente como ‘números que expresan una razón entre dos enteros’.
"La razón matemática es como una relación entre dos números que podemos comparar. Es lo que obtenemos cuando dividimos o restamos un número de otro. Las razones pueden verse como fracciones o números con punto decimal."
La notación moderna 
Ejemplos de Números Racionales
Los números racionales 
Números Enteros:
Los números enteros, como 2, y -5, son ejemplos simples de número .Cualquier número entero se puede expresar como una fracción con un denominador de 1, por ejemplo, 2/1 o –5/1.
Fracciones Comunes:
Las fracciones comunes, como 3/4 o –2/5, son números_racionales. En estas fracciones, tanto el numerador como el denominador son enteros.
Números Mixtos:
Los números mixtos son combinaciones de números enteros y fracciones. Por ejemplo, 2 1/3 se puede expresar como el número racional 7/3.
Números Decimales Finitos:
Los núm. decimales finitos, como 0.25 o -1.75, se pueden expresar como núm racionales. Para convertir un decimal finito en una fracción, basta con colocar el número decimal sobre una potencia de 10 adecuada : 25/100 = 1/4 o -1 75/100 = -1 3/4.
Números Decimales Periódicos:
Incluso los números decimales periódicos, como 1.333…, son números_racionales. Por ejemplo, 1.333… se puede expresar como 4/3.
Conclusión
En resumen, los números racionales son una parte esencial de las matemáticas y nuestra vida cotidiana. Son números que se pueden expresar como fracciones simples, ya sean positivos o negativos, enteros o fracciones. Los números_racionales tienen una rica historia que se remonta a la antigua Grecia y han desempeñado un papel crucial en el desarrollo de las matemáticas a lo largo de los siglos. Desde núm. enteros simples hasta fracciones complejas, los números_racionales nos rodean y son una herramienta fundamental en la resolución de problemas matemáticos y en la vida diaria.
¡Explora el mundo de los números_racionales y descubre su asombrosa versatilidad en la resolución de problemas matemáticos y científicos!
Números irracionales
Artículos Relacionados:

