Lo que necesitas saber sobre matemáticas:

Inicio » Matemáticas » Lo que necesitas saber sobre matemáticas:

Tiempo de lectura estimado: 15 minutos

Conceptos, trucos y aplicaciones.

Las matemáticas son una materia que puede resultar fascinante e intimidante a la vez. Desde los cálculos más sencillos hasta las ecuaciones más complejas, puede resultar difícil de entender y dominar. Sin embargo, con el enfoque adecuado y un poco de práctica, cualquiera puede aprender los conceptos, trucos y ejercicios que componen esta fascinante asignatura. En este artículo, exploraremos lo básico que necesitas saber sobre matemáticas, incluidos temas como el álgebra, el cálculo y la geometría analítica, así como algunos trucos matemáticos divertidos que puedes poner a prueba. Tanto si eres un estudiante que lucha por entender sus deberes de matemáticas, como si simplemente eres alguien que quiere aprender más sobre esta fascinante materia, este artículo tiene algo para todos. Así que, ¡vamos a sumergirnos y descubrir juntos el mundo de las matemáticas!

lo que necesitas saber sobre matemáticas

Introducción al álgebra

El álgebra es una rama de las matemáticas que trabaja con símbolos y números para abordar ecuaciones e inecuaciones. Su misión es desentrañar problemas mediante la manipulación de expresiones matemáticas. En este artículo, descubriremos los fundamentos del álgebra y sus aplicaciones en campos como la física, la ingeniería y las finanzas. Al final de esta sección, estarás familiarizado con los conceptos esenciales del álgebra y su relación con la realidad.

Ecuaciones e inecuaciones

Un tema importante del álgebra es la resolución de ecuaciones e inecuaciones. Esto implica encontrar el valor desconocido de una variable utilizando operaciones matemáticas como la suma, la resta, la multiplicación y la división. Las ecuaciones lineales, con una sola variable, son las más sencillas de resolver.

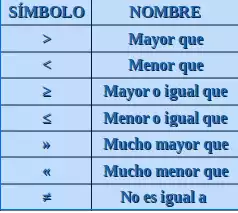
Las desigualdades, que comparan dos valores utilizando símbolos como «<«,» >»,»≠» se resuelven con un proceso similar. Dominando las técnicas de resolución de ecuaciones e inecuaciones, podrás abordar problemas algebraicos más complejos.

Las ecuaciones lineales, las funciones y las gráficas son ideas relacionadas en álgebra. Una ecuación lineal es una ecuación en la que la mayor potencia de la variable es uno. Una función es una regla que asigna una única salida a cada entrada. Una función lineal es una función cuya gráfica es una línea recta. Las gráficas se utilizan para representar la relación entre variables en una función o ecuación. Si comprendes la relación entre ecuaciones lineales, funciones y gráficas, podrás visualizar y analizar las relaciones matemáticas con mayor facilidad.

Las secuencias son series de números que siguen un patrón específico. Pueden ser aritméticas, geométricas o ninguna de ellas.

Las secuencias aritméticas implican sumar o restar un número constante a cada término para obtener el siguiente.
Las secuencias geométricas implican multiplicar o dividir cada término por un número constante para obtener el término siguiente.
Las secuencias pueden aplicarse para modelizar situaciones del mundo real, como el crecimiento de la población, los tipos de interés y los precios de las acciones. Al comprender los patrones y las propiedades de las secuencias, podrás hacer predicciones y analizar datos con mayor precisión.

Ecuaciones lineales, funciones y gráficas

Las ecuaciones lineales, las funciones y las gráficas representan un área fundamental de las matemáticas y se emplean con frecuencia en campos como la ingeniería y la física. La forma pendiente-intersección, o y = mx b, se utiliza para representar ecuaciones lineales, en las que m es la pendiente y b la intersección. Trazando dos puntos en la gráfica, se puede determinar la pendiente y la intersección, así como si dos rectas son paralelas o perpendiculares comparando sus pendientes. Las ecuaciones lineales también pueden resolverse mediante métodos de sustitución o eliminación, que consisten en sustituir una variable por una expresión en la que intervenga la otra o sumar dos ecuaciones para eliminar una variable.

Las ecuaciones y funciones lineales son aplicables en muchos ámbitos, como las finanzas, la economía y los negocios. En finanzas, las ecuaciones lineales pueden utilizarse para calcular tipos de interés y pagos de préstamos. En economía, las ecuaciones pueden emplearse para modelizar curvas de oferta y demanda. Las empresas pueden utilizar ecuaciones lineales para calcular el costo de producción y el umbral de rentabilidad. Para dominar los fundamentos de las matemáticas y aplicarlos a situaciones del mundo real, es esencial conocer a fondo las ecuaciones lineales, las funciones y las gráficas.

Secuencias

Las secuencias son un elemento fundamental de las matemáticas, que se utilizan para caracterizar listas ordenadas de números u objetos. Son una herramienta fundamental para explorar patrones y asociaciones entre números, y pueden utilizarse para resolver numerosas cuestiones en disciplinas como las finanzas, la física y la informática. Una de las características más significativas de las secuencias es su capacidad de converger o divergir, que es una noción fundamental en cálculo y análisis. Las secuencias pueden clasificarse en distintos tipos, como aritméticas, geométricas y armónicas, cada una con sus propias propiedades y ecuaciones exclusivas. Comprender las secuencias es una parte crucial del dominio de las matemáticas, y es una asignatura necesaria para quienes aspiran a seguir una carrera en los campos STEM.

**STEM** por sus siglas en ingles: Ciencia, Tecnología, Ingeniería y Matemáticas.

Una de las aplicaciones más notables de las secuencias es el estudio de las series, que son sumas totales de los términos de una secuencia. Las series pueden utilizarse para aproximar y calcular una amplia gama de funciones matemáticas, como las funciones trigonométricas y logarítmicas. Además, las series son indispensables en cálculo y análisis, donde se emplean para examinar la convergencia y divergencia de funciones. Comprender las propiedades de las secuencias y series es una parte vital del dominio de las matemáticas, y es indispensable para quienes aspiran a seguir una carrera en campos como la ingeniería, la física o la informática. Mediante el estudio de las secuencias y series, los estudiantes pueden adquirir una comprensión más profunda de los conceptos fundamentales de las matemáticas, y agudizar las habilidades necesarias para resolver problemas intrincados en una amplia gama de campos.

Sistemas de ecuaciones

Para llevar tus conocimientos de álgebra al siguiente nivel, debes dominar los sistemas de ecuaciones. Un sistema de ecuaciones es una combinación de dos o más ecuaciones que deben resolverse conjuntamente. Estas ecuaciones pueden presentar una o más variables, por lo que resolverlas suele requerir una resolución creativa de los problemas. En este artículo, trataremos los aspectos básicos de la resolución de estos sistemas y te daremos algunos consejos para que te resulte más fácil.

Un método muy utilizado para resolver sistemas de ecuaciones es la sustitución. Esto requiere resolver una ecuación para una de las variables, y luego introducir esa expresión en la otra ecuación. Entonces, se puede calcular la variable restante. Otra opción es la eliminación, que consiste en sumar o restar las dos ecuaciones para eliminar una de las variables. Dependiendo del sistema de ecuaciones, puede ser preferible cualquiera de estos métodos.

Aunque intimidante al principio, dominar los sistemas de ecuaciones es esencial en muchos campos, como la ingeniería y la economía. De hecho, muchos problemas del mundo real pueden representarse con estas ecuaciones. Comprender este concepto te dotará de las habilidades necesarias para abordar cuestiones complejas y tomar decisiones acertadas. Así que no te asustes y ponte a practicar

Inecuaciones con dos variables

El dominio de las inecuaciones con dos variables es un componente necesario de las matemáticas, que proporciona a los estudiantes una comprensión de la relación entre dos variables. Visualizar las soluciones de una inecuación utilizando un plano de coordenadas puede ayudar a los alumnos a comprender el concepto. Además, comprender las desigualdades con dos variables prepara a los alumnos para temas más complejos, como el cálculo.

Desarrollar la destreza en la resolución de inecuaciones de dos variables es esencial para el éxito en matemáticas. No sólo permite a los alumnos distinguir los signos de la pendiente de una recta, sino que también les proporciona una valiosa herramienta para abordar problemas del mundo real, en particular los que se encuentran en campos como la ingeniería y la física.

Para resolver inecuaciones de dos variables se pueden emplear varios métodos, como la representación gráfica, la sustitución y la eliminación. La representación gráfica es una opción popular, ya que permite a los alumnos visualizar las soluciones. Por su parte, la sustitución y la eliminación utilizan conocimientos algebraicos y son ideales para resolver inecuaciones más complejas. Independientemente del método utilizado, la clave del éxito reside en la práctica. Ocuparse regularmente de este tema es la forma más eficaz de ganar confianza y llegar a dominarlo.

Las desigualdades de dos variables son una parte importante de las matemáticas, con aplicaciones en economía, física e ingeniería. Familiarizarse con la forma de resolver y representar gráficamente estas inecuaciones proporciona a los alumnos una mejor comprensión de la relación entre dos variables. Este conocimiento puede aplicarse a situaciones del mundo real, lo que lo convierte en una habilidad imprescindible para cualquiera que desee seguir una carrera en un área que requiera una base sólida en matemáticas. En conclusión, dominar las inecuaciones de dos variables es esencial para tener éxito en matemáticas y como preparación para temas más avanzados.

Ecuaciones, funciones e inecuaciones de valor absoluto

Las ecuaciones, funciones e inecuaciones algebraicas de valor absoluto se encuentran entre los temas más importantes. Estas ecuaciones reflejan la distancia entre un número y el cero en la recta numérica. Resolver estas ecuaciones requiere encontrar las variables que hacen que el valor absoluto sea igual a un número dado; dichos valores pueden ser positivos o negativos.

Las funciones de valor absoluto tienen una amplia aplicación en matemáticas, y se utilizan para modelizar situaciones del mundo real en las que el resultado depende de la longitud desde un punto dado. Gráficamente, estas funciones tienen forma de V, y se abren hacia arriba o hacia abajo según el signo del coeficiente x. Para trabajar con problemas de optimización o de análisis costo-beneficio, es esencial comprender las propiedades de esta función.

Las desigualdades que implican valores absolutos también aparecen con frecuencia en matemáticas. Estas desigualdades tienen dos soluciones, situadas simétricamente alrededor del cero. Para resolverlas, hay que dividir la desigualdad en dos casos y considerar el signo de la expresión dentro del valor absoluto. Estas desigualdades se utilizan en economía, física, ingeniería y otros campos para representar límites y restricciones.

Para dominar las ecuaciones, funciones e inecuaciones de valor absoluto, hay que practicar con una variedad de problemas. Para ello, puedes acceder a recursos en línea, libros de texto y hojas de ejercicios. Recuerda que comprender el concepto es tan importante como memorizar las fórmulas o los procedimientos. Si surgen dificultades, no dudes en pedir ayuda a un tutor, profesor o amigo matemático experto.

Geometría analítica

La Geometría analítica, un campo de las matemáticas que explora la relación entre el álgebra y la geometría, es una parte integral de las matemáticas con numerosas aplicaciones prácticas. Uno de sus principios básicos es hallar la distancia y el punto medio entre dos puntos de un plano. Este concepto es útil en diversos sectores, desde la ingeniería a la física, pasando por los gráficos por ordenador.

La división de segmentos de recta es otro concepto importante de la Geometría Analítica. Esta técnica divide una línea en dos o más secciones de una relación determinada, y se utiliza en arquitectura, ingeniería y física. Por ejemplo, puede emplearse para dividir el vano de un puente en partes de igual longitud.

Las rectas paralelas y perpendiculares son otro aspecto crucial de la Geometría Analítica. Esta idea se utiliza para determinar la alineación de dos líneas, y se emplea con frecuencia en ingeniería, construcción y arquitectura para crear estructuras con líneas rectas. Las ecuaciones de rectas paralelas y perpendiculares son significativas para hallar la pendiente de una recta, lo que es importante en muchas disciplinas.

La distancia entre un punto y una recta también es un concepto fundamental de la Geometría Analítica. Se utiliza para hallar la distancia más corta entre un punto y una recta en un plano, y tiene aplicaciones en física, ingeniería e infografía. También se emplea para determinar la ubicación de un objeto en un plano, dadas sus coordenadas.

Dos trucos matemáticos que debes probar

¿Estás deseando elevar tus conocimientos matemáticos? No busques más, estos dos trucos matemáticos asombrarán y desafiarán incluso al matemático más experto.

Prueba el desafío de los Cuatro 4:

El objetivo del juego es obtener todos los números naturales del 0 al 100 usando únicamente cuatro cuatros. Las operaciones permitidas son las siguientes: suma, resta, multiplicación, división, concatenación (usar el 44 es válido y en ese caso habríamos utilizado ya dos cuatros), el punto decimal (es lícito escribir .4 si queremos poner cero coma cuatro), potencias (4⁴ está permitido, gastando así dos cuatros), raíces cuadradas, factoriales y números periódicos. También podemos usar paréntesis como creamos conveniente.

¿Puedes dominarlo? Es un ejercicio entretenido y difícil que hará fluir tu creatividad.

Adivinar el numero

Adivinarás el resultado de un numero que escojas, sin importar que números elija la otra persona.

Selecciona un número de 5 dígitos, pero el primero debe ser un 2. Escríbelo y guárdalo en tu bolsillo.

Luego, escribe en un papel otro número de 4 dígitos, por ejemplo el 3434.

Pídele a la persona que esté contigo que proponga otro número de 4 dígitos. Por ejemplo dirá 2324. Escríbelo debajo del número que propusiste en el paso anterior.

Después tú eliges otro número de 4 dígitos: 7675

Vuelves a pedirle a la persona que proponga otro número aleatorio de 4 dígitos, por ejemplo 8634

Finalmente tú colocas otro número de 4 dígitos debajo: 1365

Sumas los cinco números. Y el resultado es 23432. Revisa tu bolsillo. ¿Es el mismo número?¿Sorprendido?

La explicación

Recuerda que tienes que construir el número clave de 5 dígitos con el número 2 al principio. Ese es el que guardas en tu bolsillo, por ejemplo 23432.

Cuando propones el primer número de cuatro dígitos tiene que tener cierta particularidad. Debe comenzar con los 3 números centrales, es decir 343 y el último dígito debe ser también el último de tu número clave más 2. Por lo que sería 2+2=4. El primer número que propondrás será 3434.

El número que elije tu compañero/a es aleatorio.

Pero el que tú selecciones inmediatamente después depende del número que él eligió. Y cada dígito deberá completar 9. Es decir, si optó por el 2324, tú debes escribir 7675 debajo porque 2+7=9; 3+6=9; 2+7=9; 4+5=9.

La otra persona elige el siguiente número y tú repites el mismo procedimiento con el tuyo completando 9 en cada dígito. Es decir, si tu compañero escogió 8634, tú escribes 1365. (8+1=9; 6+3=9; 3+6=9; 4+5=9)

Al final, sumas todas las cifras y el resultado será el número del papel en tu bolsillo 23432.

Matemáticas de secundaria

Las matemáticas de secundaria son una asignatura esencial que sienta las bases para cursos de matemáticas más avanzados. Incluye el estudio del álgebra, la geometría, la trigonometría y el cálculo. Este artículo explorará por qué es tan importante dominar las matemáticas de secundaria antes de progresar a temas más complejos.

Una de las principales ventajas de estudiar matemáticas de secundaria es que ayuda a cultivar la capacidad de pensamiento crítico. Al abordar problemas intrincados, los alumnos pueden aprender a examinar la información, discernir patrones y sacar conclusiones lógicas. Estas habilidades resultan útiles no sólo en matemáticas, sino también en otras disciplinas y en la vida cotidiana.

Una razón adicional para estudiar matemáticas en secundaria es que constituyen la base de los cursos de nivel superior, por ejemplo cálculo, estadística y álgebra lineal. Sin un buen dominio de los conceptos básicos, los alumnos podrían tener dificultades para comprender material más avanzado. Además, numerosas universidades y escuelas superiores exigen que los aspirantes posean un cierto grado de aptitud matemática para matricularse en determinados programas, como ingeniería o informática.

Por último, las matemáticas en secundaria pueden ser divertidas y gratificantes. Al dominar la asignatura, los estudiantes pueden obtener una sensación de logro y confianza que pueden trasladar a otras partes de su vida. Además, las matemáticas son un campo versátil e interdisciplinar con una amplia gama de aplicaciones, desde la física y la ingeniería hasta la economía y la informática.

Cálculo

El cálculo es un pilar esencial de las matemáticas y, al mismo tiempo, uno de los más difíciles de conquistar. Implica el examen de las tasas de transformación y colección, y se aplica en una amplia gama de ámbitos, desde la física y la ingeniería hasta la economía y la biología. El cálculo se divide en dos ramas principales: el cálculo diferencial, que estudia las tasas de alteración y las inclinaciones de las curvas, y el cálculo integral, que analiza la acumulación y el área bajo curvas. Para ser competente en cálculo se requiere una sólida comprensión del álgebra, la trigonometría y la geometría, junto con una paciencia inquebrantable y mucha práctica.

La derivada

Un concepto primordial del cálculo es la derivada, una medida de cómo cambia una función. Esta derivada se expresa como el límite de la fracción de la transformación en la función respecto a la transformación en la variable independiente a medida que esta última tiende a cero. La derivada puede emplearse para localizar el gradiente de la recta tangente a la curva en cualquier punto, así como para determinar los valores mínimo y máximo de la función. Además, se utiliza para analizar dificultades de optimización, por ejemplo reconocer el valor máximo o mínimo de una función sujeta a restricciones definidas.

La integral

Otro concepto significativo en cálculo es la integral, una medida del área bajo una curva. Esta integral se representa como el límite de la suma de las áreas de un número infinito de rectángulos a medida que la anchura de los rectángulos se aproxima a cero. La integral de una función puede utilizarse para hallar el cambio global o acumulación de la función en un intervalo concreto, así como para hallar el valor medio de la función en ese intervalo. Además, se emplea para estudiar problemas de movimiento, como descubrir la distancia recorrida o la velocidad de un objeto en un momento dado.

Conclusión

En conclusión, las matemáticas son una materia amplia y fascinante que tiene aplicaciones en casi todos los aspectos de nuestra vida. Desde resolver ecuaciones básicas hasta explorar las complejidades del cálculo, siempre hay algo nuevo que descubrir y aprender. Tanto si eres un estudiante que lucha por comprender un concepto como un entusiasta de las matemáticas que quiere probar algunos trucos nuevos, la práctica es clave para dominar esta materia. Así pues, sigamos explorando el mundo de las matemáticas, apreciando su belleza y utilidad, y esforzándonos por mejorar nuestras habilidades mediante el esfuerzo y la dedicación constantes.