La trigonometría es una rama esencial de las matemáticas que se ocupa del estudio de los ángulos y triángulos. Desempeña un papel crucial y tiene aplicación en diversos campos, como la ingeniería, la física, la arquitectura y la astronomía. En este artículo exploraremos el concepto de trigonometría, sus funciones y aplicaciones. También examinaremos cómo los triángulos rectángulos son la base de muchas ideas en geometría y trigonometría. Así pues, acompáñanos mientras profundizamos en el mundo de los triángulos y descubrimos las maravillas de la trigonometría.
Definición de trigonometría
La trigonometría, derivada de las palabras griegas trigonon (triángulo) y metron (medida), es un área de las matemáticas que estudia las propiedades de los triángulos. Permite medir ángulos, distancias y alturas de diversos objetos, y es un componente clave en varios campos, como la ingeniería, la física, la navegación y la astronomía. Mediante el uso de las razones seno, coseno y tangente de los triángulos rectángulos, así como de sus funciones inversas (cotangente, secante y cosecante), la trigonometría es aplicable en el diseño y construcción de estructuras, gráficos por ordenador y animación.



Una comprensión profunda de la definición de trigonometría es esencial para entender sus aplicaciones en el mundo real. Esta rama de las matemáticas proporciona la base para medir los ángulos y lados de un triángulo, y se utiliza en muchos aspectos de la ciencia y la tecnología. Su utilidad puede verse en la creación de edificios, puentes y otras construcciones, así como en el avance de los gráficos y la animación por ordenador.
Usos de la trigonometría
La trigonometría es una disciplina matemática vital con numerosas aplicaciones en la navegación, la topografía, la ingeniería y la arquitectura. Los arquitectos la utilizan para calcular la altura y la distancia de los edificios, garantizando la integridad estructural de sus planos. En física, se utiliza para calcular la posición, velocidad y aceleración de objetos en movimiento, sobre todo en el movimiento de proyectiles. También se emplea en gráficos por ordenador para especificar los ángulos y proporciones de objetos tridimensionales, que se utilizan para hacer animaciones y efectos especiales. Por último, los astrónomos utilizan la trigonometría para calcular las distancias y los ángulos entre cuerpos celestes, lo que ayuda a determinar el tamaño, la forma y la distancia de planetas, estrellas y galaxias.
Funciones trigonométricas
Las funciones o razones trigonométricas son una parte esencial de la trigonometría, ya que proporcionan una forma de relacionar los ángulos de un triángulo rectángulo con las longitudes de sus lados. Estas ecuaciones también pueden extenderse a triángulos no rectángulos y a números complejos, lo que las hace muy valiosas en muchas disciplinas. Las principales funciones trigonométricas son el seno, el coseno y la tangente, que representan las relaciones de los lados opuestos, adyacentes e hipotenusa de un triángulo rectángulo. Otras funciones importantes son la cotangente, la secante y la cosecante, que son las recíprocas de las funciones primarias. Comprender estas ecuaciones es esencial para resolver problemas relacionados con ángulos y distancias en campos como la ingeniería, la física y la astronomía.
Las funciones trigonométricas tienen numerosas aplicaciones en muchas áreas, como la astronomía, la física, la ingeniería y la arquitectura. La astronomía las utiliza para calcular las distancias entre estrellas y planetas, así como para determinar la posición de los objetos celestes en función de sus ángulos y distancias a la Tierra. La ingeniería recurre a ellas para calcular las fuerzas y tensiones en estructuras y máquinas, mientras que en arquitectura se utilizan para diseñar edificios y estructuras estables y seguros. Las funciones trigonométricas también se utilizan en teoría musical, gráficos por ordenador y desarrollo de juegos.

Las funciones trigonométricas se definen como las relaciones entre los lados de un triángulo rectángulo y los ángulos opuestos o adyacentes a ellos. Estas ecuaciones se basan en las características de los triángulos rectángulos, que tienen un ángulo igual a 90 grados. El estudio de los triángulos rectángulos y sus propiedades constituye la base de la trigonometría, ya que permite relacionar los ángulos de un triángulo con las longitudes de sus lados.

Las funciones trigonométricas también pueden expresarse en términos de radianes, que son una medida de ángulos basada en el radio de un círculo. Esto simplifica muchos cálculos y permite mediciones más precisas de los ángulos en trigonometría y otras áreas de las matemáticas y la ciencia.
Triángulos rectángulos y trigonometría
Como se mencionaba al inicio del artículo, la trigonometría estudia las relaciones entre los elementos de los triángulos rectángulos. Uno de los ángulos de dichos triángulos mide 90 grados y dos de sus lados son adyacentes a él. La hipotenusa es el lado opuesto al ángulo de 90 grados, mientras que los otros dos se denominan catetos. A partir de las relaciones entre los lados de un triángulo rectángulo, la trigonometría define las funciones trigonométricas, como el seno, el coseno y la tangente. Estas funciones se emplean para responder a preguntas relacionadas con ángulos y distancias en muchas disciplinas, como la astronomía, la ingeniería y la física.
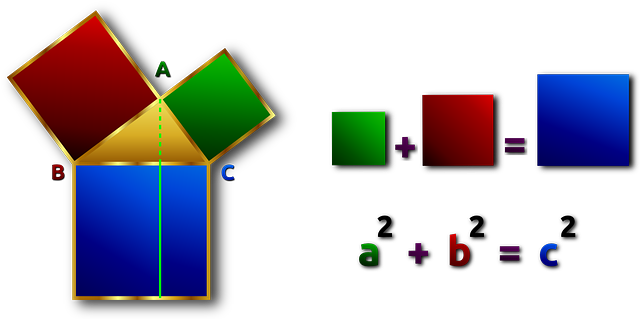
El teorema de Pitágoras es una piedra angular de la trigonometría que resulta útil para determinar la longitud de los lados de un triángulo rectángulo. Este teorema establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de sus catetos. Por tanto, conociendo la longitud de dos lados de un triángulo rectángulo, el teorema nos permite averiguar la longitud del tercer lado. Se utiliza mucho en aplicaciones de la trigonometría como calcular la distancia entre dos puntos en un plano de coordenadas y estimar la altura de un edificio a distancia.
La trigonometría es indispensable en muchos campos que requieren el uso de la geometría, como la arquitectura, la ingeniería y la física. Los arquitectos la emplean para diseñar edificios de formas intrincadas y calcular los ángulos y distancias de sus elementos. Los ingenieros la utilizan para construir y evaluar estructuras como puentes y torres, así como para calcular las fuerzas y tensiones que pueden soportar. Los físicos recurren a la trigonometría para describir el movimiento de los objetos en el espacio, calcular la velocidad y dirección de los cuerpos en movimiento y estudiar las ondas y vibraciones. Esto hace que un conocimiento profundo de la trigonometría y sus aplicaciones sea esencial para cualquier persona que quiera hacer carrera en estas áreas.
Relaciones trigonométricas
Las proporciones trigonométricas ocupan un papel crucial en el examen de la trigonometría. Estas proporciones se emplean para detectar las conexiones entre los ángulos y los lados de un triángulo rectángulo. Las tres proporciones trigonométricas principales son el seno, el coseno y la tangente. Estas proporciones se definen como las proporciones entre los lados de un triángulo rectángulo, y nos ayudan a reconocer los ángulos y las distancias que intervienen en diversos problemas relacionados con la trigonometría.
Empleando las razones trigonométricas, podemos evaluar la medida de un lado que falta de un triángulo rectángulo, dadas las longitudes de los otros dos lados, o podemos hallar la medida de un ángulo, dadas las longitudes de dos lados. Estas proporciones son indispensables en una gran variedad de campos, como la astronomía, la ingeniería, la física y la arquitectura.
Las proporciones trigonométricas se utilizan para resolver problemas relacionados con alturas y distancias. Por ejemplo, para establecer la altura de un edificio alto, puedes emplear la razón tangente. Mides el ángulo de elevación desde el suelo hasta la parte superior del edificio, y luego mides la distancia desde la base del edificio hasta donde te encuentras. Utilizando la razón tangente, puedes calcular la altura del edificio.


Las razones trigonométricas también se emplean en la navegación. Las razones seno y coseno se utilizan para determinar la posición de un barco o un avión. Los pilotos y navegantes utilizan estas razones para decidir la dirección y velocidad de un avión, y la distancia entre dos puntos.

Conclusión
En conclusión, la trigonometría es una fascinante rama de las matemáticas que tiene numerosas aplicaciones en campos como la astronomía, la ingeniería y la física. Estudiando las relaciones entre los elementos de un triángulo rectángulo, podemos comprender el mundo que nos rodea de una forma más profunda. Tanto si calculamos distancias entre planetas como si diseñamos edificios, la trigonometría desempeña un papel crucial en la sociedad moderna. Utilizando los conceptos y funciones de la trigonometría, podemos resolver problemas complejos y comprender mejor el universo en que vivimos.

