Tiempo de lectura estimado: 8 minutos
Bienvenido a nuestro artículo Explorando el concepto del Teorema de Pitágoras. Si eres un entusiasta de las matemáticas o simplemente sientes curiosidad por el mundo de los triángulos, has aterrizado en el lugar adecuado. El teorema de Pitágoras es un concepto fundamental en el ámbito de las matemáticas, y ha sido una piedra angular de la educación durante siglos. En este artículo, nos sumergiremos en la definición, la historia y las aplicaciones prácticas del teorema de Pitágoras, y exploraremos distintas formas de demostrar y comprender este principio matemático. Así pues, embarquémonos en este viaje de descubrimiento y desentrañemos los misterios de los triángulos con el teorema de Pitágoras.
¿Qué es el Teorema de Pitágoras?
El Teorema de Pitágoras es una parte integral de las matemáticas con muchas aplicaciones en diversos campos. Este teorema explica la conexión entre los lados de un triángulo rectángulo, y se expresa matemáticamente como a2 + b2 = c2 donde c es la hipotenusa, y a y b son los catetos. Desde el cálculo de la diagonal de una pantalla de TV hasta la determinación de la longitud de una escalera necesaria para alcanzar cierta altura, el teorema es aplicable en una gran variedad de escenarios. Incluso determinar la distancia entre dos puntos de un plano de coordenadas implica el uso del Teorema de Pitágoras. Este antiguo concepto, cuya importancia persiste en el mundo moderno, ofrece una visión de la relación entre los lados de un triángulo rectángulo y su significado en nuestras vidas.
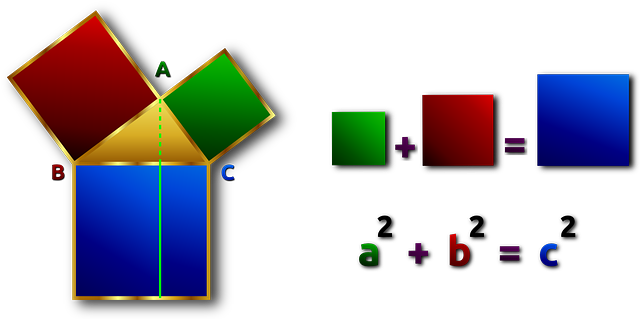
No se puede exagerar la utilidad del Teorema de Pitágoras. Es un concepto versátil con aplicaciones en física, ingeniería y arquitectura, por nombrar algunas. Su importancia es evidente en nuestra vida cotidiana, desde medir la anchura diagonal de un televisor hasta calcular la longitud de una escalera. Incluso las tareas más mundanas, como determinar la distancia entre dos puntos en un plano de coordenadas, requieren el uso de este teorema. Comprender el Teorema de Pitágoras puede ayudarnos a apreciar la relación entre los lados de un triángulo rectángulo y su relevancia en nuestras vidas.
Aplicaciones matemáticas en la vida cotidiana
Las matemáticas impregnan todos los ámbitos de nuestra vida, desde determinar la superficie de una habitación hasta medir la distancia entre dos puntos. Cabe destacar la importancia del teorema de Pitágoras, que tiene muchas aplicaciones en el mundo real. Los arquitectos e ingenieros, por ejemplo, lo utilizan para construir edificios y estructuras robustas y seguras. Aprovechando el Teorema de Pitágoras, pueden evaluar con precisión la longitud de cada lado de un triángulo rectángulo, garantizando así la estabilidad y la resistencia a las fuerzas externas.
El teorema también tiene su utilidad en la navegación. Pilotos y marineros lo utilizan para calcular la distancia entre dos puntos, como la altitud de un avión respecto al suelo o la distancia que separa un barco de un faro. Utilizando el Teorema de Pitágoras y otros principios matemáticos, son capaces de trazar su rumbo y llegar a su destino sin incidentes.
Los deportistas también encuentran útil el Teorema de Pitágoras. Los jugadores de baloncesto lo utilizan para calcular su distancia a la canasta, de modo que puedan calcular el ángulo preciso y la trayectoria necesaria para un tiro acertado. Del mismo modo, los golfistas lo emplean para medir su distancia al hoyo, ayudándoles a elegir el palo ideal para su golpe.
Historia del Teorema de Pitágoras
Se atribuye a Pitágoras, matemático griego, el descubrimiento de uno de los conceptos matemáticos más antiguos, conocido como teorema de Pitágoras. Sin embargo, se cree que los babilonios y los egipcios conocían la relación entre los lados de un triángulo rectángulo mucho antes que él. Se pueden encontrar ejemplos de triángulos rectángulos en antiguas construcciones egipcias de miles de años de antigüedad. Posteriormente, el teorema fue perfeccionado por numerosos matemáticos, siendo Euclides quien aportó la primera demostración de la que se tiene constancia.
El periodo renacentista marcó un hito importante en el estudio del teorema de Pitágoras, con figuras de renombre como Leonardo da Vinci y Galileo Galilei explorándolo ampliamente. Además, su influencia se extendió a otros campos como la música y el arte. Por ejemplo, el sistema pitagórico de afinación se ideó basándose en el teorema y se utilizó en la música durante siglos. Además, se empleó para generar dibujos y pinturas en perspectiva en el arte.
En la actualidad, el teorema de Pitágoras sigue siendo una parte esencial de la enseñanza de las matemáticas. Considerado como uno de los elementos básicos de la geometría, se enseña a estudiantes de todo el mundo. Aparte de sus funciones prácticas, el teorema también ha tenido un impacto considerable en el avance de las matemáticas como disciplina. La historia del teorema de Pitágoras demuestra la importancia de las ideas matemáticas y cómo conforman nuestra percepción del entorno.
Formulación del teorema de Pitágoras
El teorema de Pitágoras es un concepto fundamental y de larga tradición en matemáticas. Fue formulado por Pitágoras, que percibió la relación entre los lados de un triángulo rectángulo. El teorema se expresa como a² b² = c², donde los catetos son a y b, mientras que c es la hipotenusa. Esta fórmula es fundamental para resolver cuestiones relacionadas con los triángulos rectángulos, y tiene diversas aplicaciones prácticas en la vida cotidiana.
Pitágoras y sus alumnos fueron los primeros en demostrar que la correlación entre los lados de un triángulo rectángulo era coherente. Sin embargo, el teorema de Pitágoras ha sido confirmado utilizando diversos enfoques. Puede demostrarse mediante manipulaciones algebraicas, construcciones geométricas e incluso pruebas asistidas por ordenador. Estas diversas demostraciones han ayudado a profundizar en la comprensión matemática y a explorar más el concepto.
Aunque el teorema de Pitágoras se utiliza ampliamente en la educación, tiene ciertas restricciones. Sólo se refiere a triángulos rectángulos, y no se refiere directamente a la longitud de la hipotenusa. Además, el teorema sólo es válido en el espacio plano euclídeo. Las distintas geometrías, como el espacio curvo o no euclidiano, tienen conexiones distintas entre los lados de un triángulo rectángulo y no se atienen al teorema de Pitágoras.
El Teorema de Pitágoras tiene una abundante historia y ha sido empleado en múltiples campos de estudio. Es un concepto esencial en matemáticas y ha influido en muchas otras áreas del conocimiento. Comprender la formulación del teorema de Pitágoras es imprescindible para resolver problemas con triángulos rectángulos, y ayuda a visualizar la relación entre los lados de un triángulo rectángulo.
Demostraciones del Teorema de Pitágoras
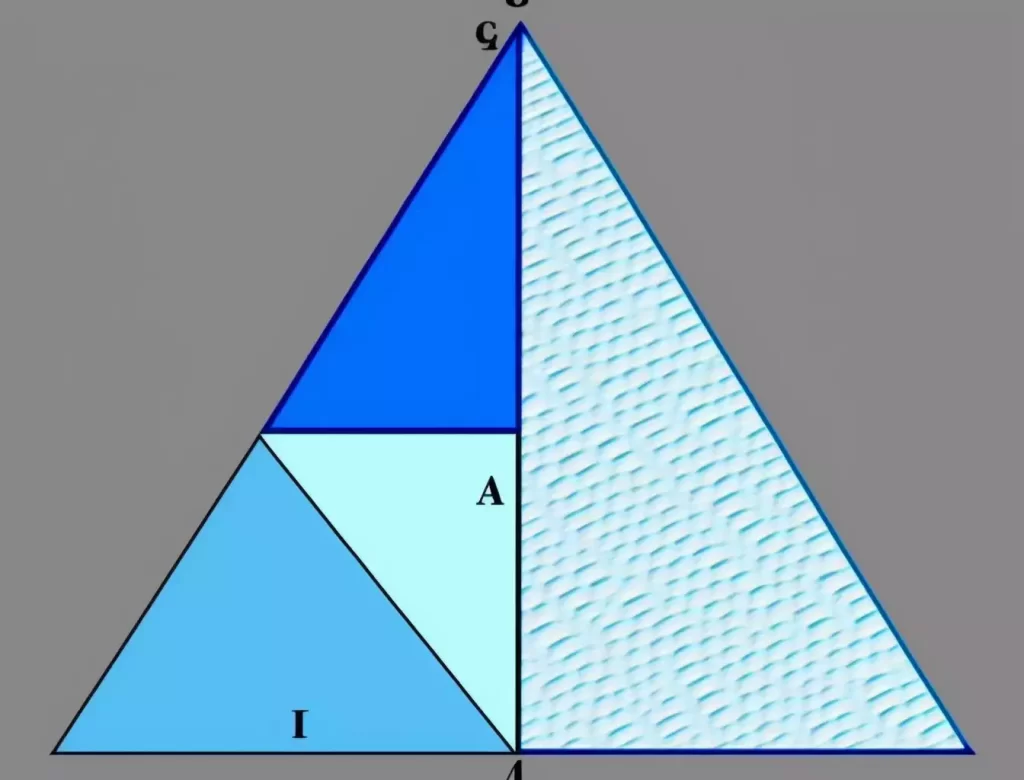
Matemáticos y educadores han explorado numerosas formas de demostrar el Teorema de Pitágoras a lo largo de los siglos. Un enfoque popular es la Demostración Geométrica, que utiliza cuadrados para representar las áreas laterales del triángulo. Este método visual presenta el concepto a los alumnos. Otra demostración es la Algebraica, que se basa en ecuaciones para demostrar el teorema, y demuestra su aplicabilidad a todos los triángulos rectángulos.
Una demostración emocionante del Teorema de Pitágoras es la Demostración Trigonométrica. Este proceso utiliza funciones trigonométricas para demostrar la relación entre los lados y los ángulos del triángulo. Además, el teorema puede demostrarse mediante Triples Pitagóricos, un conjunto de tres números enteros que lo satisfacen. Este método muestra las aplicaciones prácticas del teorema en la ingeniería y la construcción. En conclusión, existen múltiples demostraciones del Teorema de Pitágoras, cada una con su propio enfoque y propósito únicos, lo que lo convierte en un concepto intrigante que explorar.
Limitaciones del Teorema de Pitágoras
El Teorema de Pitágoras es una venerable herramienta matemática que se ha utilizado durante siglos para resolver rompecabezas relacionados con triángulos rectángulos. Sin embargo, cabe señalar que el teorema tiene sus restricciones. Una limitación primordial es que sólo se aplica a los triángulos rectángulos, por lo que quienes intenten resolver problemas con triángulos no rectángulos deben recurrir a otros métodos para descubrir la longitud de los lados.
Además, el Teorema de Pitágoras no tiene en cuenta la curvatura de la Tierra. Por tanto, no puede utilizarse para calcular con precisión distancias a grandes distancias sobre la superficie de la Tierra. Para resolver este problema, los geógrafos y topógrafos utilizan una fórmula diferente conocida como fórmula de Haversine, que tiene en cuenta la curvatura de la Tierra. No obstante, el Teorema de Pitágoras sigue siendo una herramienta importante en matemáticas y sus aplicaciones se siguen explorando y ampliando.
Conclusión
En conclusión, el Teorema de Pitágoras es un concepto fundamental en matemáticas que tiene aplicaciones prácticas en la vida cotidiana. Su historia se remonta a la antigüedad, y se utiliza ampliamente en la enseñanza para resolver problemas con triángulos rectángulos. Aunque el teorema tiene limitaciones y sólo se aplica a los triángulos rectángulos, sigue siendo una herramienta esencial en los cálculos matemáticos. Explorando el concepto del teorema de Pitágoras, podemos comprender mejor la relación entre los lados de un triángulo rectángulo y su hipotenusa.

